المربع هو شكل هندسي رباعي أحدب، وهو من الأشكال الهندسية المغلقة، ويتكون المربع من أربع أضلاع متساوية في الطول، يتعامد كل ضلع فيه على الآخر مكونا زاوية قياسها 90°، أي أن المربع به 4 زوايا متساوية في القياس، ومجموع زواياه الداخلة تساوي 360°.
خصائص المربع
- يتكون المربع من أربع أضلاع متساوية في القياس، وأربع زوايا قائمة قياس كلا منها 90°.
- مجموع قياسات زوايا المربع الداخلة 360° لأنه شكل هندسي مغلق يزيد عدد أضلاعة عن 3 أضلاع.
- كل ضلعين متقابلين في المربع متوازيين، وكل ضلعين متجاورين متعامدين.
- المربع له قطران فقط ويكونا متعامدان ومتساويان في الطول، وينصف كلا منهما الزاويتين الواصل بينهما.
- المربع له 4 محاور تماثل تقسمه إلى جزئين متطابقين، حيث يعتبر القطرين محاور تماثل، ويمكن رسم محورين آخرين يصلان كل ضلعين متقابلين ليقسم كل منهما المربع إلى مستطيلين متطابقين.
- المربع هو متوازي أضلاع فيه كل ضلعين متقابلين متوازيين ومتساويين وفي الطول، وفيه كل زاويتين متقابلتين متساويتان في القياس.
- المربع هو مستطيل جميع أضلاعه متساوية في القياس.
- المربع هو معين جميع زواياه قائمة.
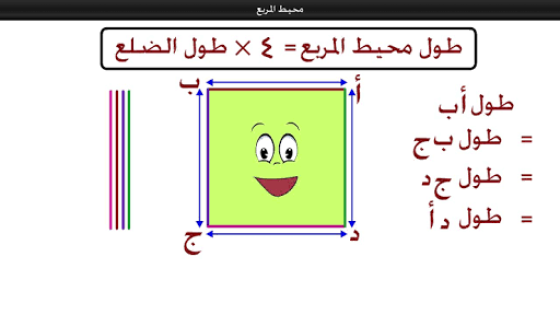
- محيط المربع يساوي مجموع أطوال أضلاعه أو حاصل ضرب طول الضلع × 4.
- مساحة المربع يساوي حاصل ضرب طول الضلع × نفسه.
ما هو محيط المربع؟
محيط المربع يساوي مجموع أطوال أضلاعه، حيث أن هذا هو القانون الثابت لحساب محيط أي شكل هندسي، وإذا افترضنا وجود مربع abcd فيمكننا حساب محيطه عبر جمع طول الضلع ab + طول الضلع bc + طول الضلع cd + طول الضلع ad، ويقاس محيط المربع بنفس وحدة القياس المستخدمة في أطوال الأضلاع.
بما أن جميع أطوال أضلاع المربع متساوية في القياس كما ذكرنا مسبقا، فيمكننا حساب المحيط من خلال ضرب طول الضلع × عدد الأضلاع، وبناء على ذلك فإننا نستنتج أنه يمكننا الإجابة على سؤال “ما هو محيط المربع؟” من خلال القانون التالي: محيط المربع = طول الضلع × 4 .
مثال: قطعة أرض صغيرة مربعة الشكل طول ضلعها 50 متر، إحسب محيطها.
محيط المربع = 50 × 4 = 200 متر.
مساحة المربع
مساحة المربع هي المساحة الكلية داخل المربع، ويمكن حساب مساحة المربع من خلال القانون طول الضلع × طول الضلع، وبالتالي يكون قانون حساب مساحة المربع كالتالي: مساحة المربع = طول الضلع × نفسه، أو (طول الضلع)²، وتقاس مساحة المربع بالوحدة مربعة.
يمكن حساب مساحة المربع من خلال إيجاد مساحة المثلثين بداخله وذلك عبر رسم قطر للمربع ليقسمه إلى مثلثين متطابقين، ثم نحسب مساحة كل مثلث على حدة عبر القانون مساحة المثلث = 1/2 × طول القاعدة × الارتفاع، ثم نضرب الناتج × 2 ويكون الناتج هو مساحة المربع الكلية.
وإذا كانت معطيات المسألة بها طول القطر والمطلوب إيجاد طول الضلع، في هذه الحالة يمكننا إيجاد طول الضلع باستخدام نظرية فيثاغورث، والتي تنص على “في المثلث القائم الزاوية، فإن (طول القطر)² = (طول الضلع الأول)² + (طول الضلع الثاني)²، وبما أن أطوال أضلاع المربع متساوية في الطول فإن طول الضلع يساوي:
(طول الضلع)² = (طول الوتر)² – (طول الضلع)²
أمثلة على محيط المربع
مثال 1: لوحة مربعة الشكل، محيطها 20 متر احسب مساحتها.
محيط المربع = طول الضلع × 4 بالتعويض في المسألة
20 = طول الضلع × 4
طول الضلع = 20 ÷ 4 = 5 متر.
مساحة المربع = طول الضلع × نفسه
مساحة المربع = 5 × 5 = 25 متر².
مثال 2: ورقة مربعة الشكل، طول ضلعها يساوي 10 سم، احسب محيطها ومساحتها.
محيط المربع = طول الضلع × 4
محيط المربع = 10 × 4 = 40 سم.
مساحة المربع = طول الضلع × نفسه
مساحة المربع = 10 × 10 = 100 سم².